9639. Большой массив Дино

Однажды когда Дино решал задачу, связанную с массивами, он увидел что размер всех массивов равен самое большее 10⁶. Так как Дино является динозавром, ему это число показалось очень маленьким. Поэтому он решил создать большой массив.

Дино сначала создает пустой массив и выбирает n пар чисел: (a₁, b₁), (a₂, b₂), ..., (a_n, b_n). Затем для каждой из этих пар он вводит в массив число b_i в количестве a_i. Например, если первая пара будет (3, 5), то в массив число 5 будет введено 3 раза. После этого Дино решает расположить данный массив в неубывающем порядке, но так как массив очень большой, компьютер Дино не может выполнить данное расположение. Ему интересно в данном упорядоченном массиве k-ое (массив нумеруется с числа 1) число. Помогите Дино найти данное число.

Вход. В первой строке задано целое число n (1 ≤ n ≤ 10⁵). В каждой из следующих n строк содержится пара (a_i, b_i) (1 ≤ a_i, b_i ≤ 10⁵). Последняя строка содержит число k. Гарантировано, что существует k-ое число в массиве.

Выход. Выведите k-ое число в неубывающем массиве.

Пример входа	Пример выхода
3 1 2 3 6 2 1 3	2

РЕШЕНИЕ

структура данных map

Анализ алгоритма

Объявим структуру данных map. Для каждой пары (a_i, b_i) добавим a_i к m[b_i]. Ключами отображения будут числа в массиве, ассоциированными значениями – количество раз, которое ключ встречается в массиве.

Суммируем количество элементов в массиве, перебирая map с наименьшего ключа и складывая ассоциированные значения. Как только сумма достигнет значения k, ключ (k-ый элемент массива) будет найден.

Пример

Отображение map после добавления трех пар из примера будет иметь следующий вид:

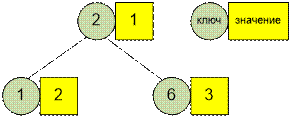
Массив в примере содержит две 1, одну 2 и три 6. Третьим элементом после сортировки будет 2.

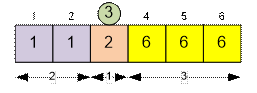
Рассмотрим процес поиска третьего элемента (k = 3) в массиве.

1 Итерация. k = 3, m[1] = 2. Проверяем: m[1] ≥ 3? Нет, вычитаем m[1] из k, k = 3 – 2 = 1.

2 Итерация. k = 1, m[2] = 1. Проверяем: m[2] ≥ 1? Да, искомым элементом массива является ключ текучей вершины map, то есть число 2.

Реализация алгоритма

Объявим структуру данных map.

map<int, long long> m;

Читаем входные данные. Для каждой пары (a_i, b_i) добавим a_i к m[b_i].

scanf("%d", &n);

for (i = 0; i < n; i++)

{

scanf("%d %d", &a, &b);

m[b] += a;

}

Перебираем структуру map в порядке возрастания ключей. Вычитаем из k ассоциированные значения. Как только ассоциированное значение для очередного ключа будет не меньше k, то соответствующий ему ключ является k-ым элементом массива.

scanf("%lld", &k);

for (iter = m.begin(); iter != m.end(); iter++)

{

if ((*iter).second >= k) break;

k -= (*iter).second;

}

Выводим ответ.

printf("%d\n", (*iter).first);